Setup

Register for the lab using grinch: https://grinch.caltech.edu/register and clone the repository as explained in the setup instructions.

Goals and Outcomes

In this lab, you will write a machine learning algorithm that uses a tree!

By the end of this lab, you will…

be more familiar with basic tree algorithms
have written a basic machine learning algorithm

Machine Learning with Decision Trees

Machine learning (ML) is all about using patterns in data to solve problems that are difficult to mathematically pin down manually. Given an input, we’d like to predict the “right” outcome using a model. This is where trees come in! One way of modeling a complex function in an intuitive manner is with a decision tree. You will code up the Iterative Dichotomizer 3 (ID3) algorithm in this lab.

ID3 Algorithm

In this lab, we will try to predict if a passenger survived the Titanic disaster. We will use several (problematic) attributes of the passengers (e.g., “age”), and predict their outcome (e.g., dead or alive).

To do this, we will build a tree where each non-leaf node represents an attribute and each leaf node represents an outcome.

For example, ID3 might output a tree that looks like the following:

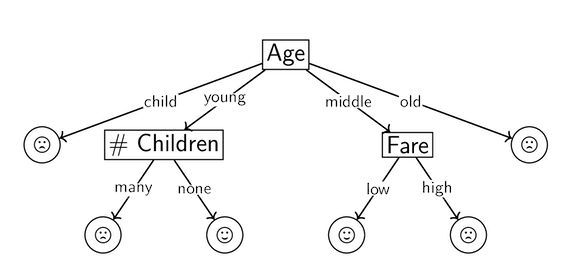
titantic

We need some metric to decide how to build our decision tree from the available attributes–which attributes do we want to split on earlier, and which are we okay leaving for later?

Entropy is a fitting metric for such a decision tree: it is the expected value of information content when measuring the outcome of an event. By minimizing entropy as we build the tree from the root, we can narrow down from the more general attributes to the more specific ones and thus minimize uncertainty. We used a similar metric for predicting “englishness” in project01, like last time, you won’t have to compute entropy yourself.

For this lab, you will need to use methods from the Dataset class. To do this, read the documentation, but not the code in that class.

The pseudocode for constructing the ID3 decision tree is as follows:

id3helper(data, attributes):

If all the remaining data points have the same outcome:
- Return an outcome node with this outcome
If there are no remaining attributes:
- Return an outcome node with the most common outcome
Find the lowest entropy attribute, \(a\).
For each feature, \(f\), of \(a\):
- Find all the data points that have the feature \(f\).
- If there are none:
  - Guess! Make an outcome child with the most common outcome.
- Otherwise:
  - Use the data! Recursively make a child out of the remaining data points, using all attributes except for \(a\).
Return the attribute node with the children generated above.

Task 0. Write the id3 method in DecisionTree.java to the specification above.

Task 1. Once the decision tree is built, it’s time to predict! Given a data point, we traverse the decision tree until we hit a leaf node. Implement this tree traversal recursively as the predict method in DecisionTree.java.

Checking the Results on `gitlab`

Task 2. Check to make sure you are passing all the tests on gitlab.

Getting Checked Off

At the end of every lab, you will need to call over a member of course staff to review your work. Sometimes, we will ask you to think about questions that you’ll review with the person who checks you off. For this lab, please answer the following questions: