Goals and Outcomes
In this project, you will build a guitar simulator which synthesizes guitar-like sounds using various data structures.
By the end of this project, you will…
- gain an understanding of the usage of backing arrays and linked lists in data structures
- learn multiple methods of implementing a stack, queue, and deque and analyze the pros/cons of each method
- understand the power of abstraction in breaking down a problem and implementing a solution
Connection to Lecture
This project is covers lecture03 through lecture06. You will likely find the code from these lectures to be very useful in this project.
Overview and Implementation Strategy
In the previous two projects, you were a client of the built-in Java data structures in java.util. One of the main goals of the next series of
projects is to build your own versions of these data structures (i.e., be the implementor rather than the client). In this project, you will begin this
process by building your own versions of the list-like structures. In particular, you will implement three different versions of stacks and queues.
After you’ve implemented the data structures, you will build a program to simulate the plucking of a guitar string. Your sound synthesizer will use your data structures to back the algorithm.
It should go without saying that you may not use any of the built-in java.util data structures! The whole point is to build your own versions! You may import java.util.Iterator, though.
As you are implementing the data structures, it will be extremely helpful to read the documentation in the interface files. Otherwise, it is very likely you will have no idea what to do!
Stacks, Queues, and Deques
We saw stacks and queues in lecture, but, in this project, you will implement a generalization of them called a deque (prounounced “deck”). A deque is a “double-ended queue” which allows you to add and remove from both ends. Another way of looking at deques is that they are simultaneously stacks (LIFO data structures) and queues (FIFO data structures). Just like with lists, there are multiple implementations of deques: an array-based implementation and a node-based implementation. We will begin with implementing these.
Task 0.
Begin by opening the interfaces folder in IntelliJ and reading the documentation in the IDeque.java file. We will not repeat information that is in these interface files
in the specification–so, it is on you to make sure you are reading these files as you complete the project. You should not edit these files. You will be editing the files in the
datastructures package.
Seriously. Do not skip this step. You will end up spending hours confused if you skip this step. Please!
ArrayDeque Requirements
Your ArrayDeque class should implement the IDeque, IQueue, and IStack interfaces using a backing array (not an ArrayList!) to store the data.
Your data structure should have a default initial capacity of 10 items and grow when it runs out of internal capacity. You should also override the toString
method to output the canonical list representation we used in lecture. You should implement the following two constructors:
public ArrayDeque()
Initializes the ArrayDeque with the default initial capacity of 10.
public ArrayDeque(int initialCapacity)
Initializes the ArrayDeque with the initial capacity of initialCapacity.
One of your constructors should call the other one using the this() notation discussed in lecture. The tests will check for this.
When you choose the design of your ArrayDeque, keep the following restrictions in mind:
- All stack methods should run in constant time with respect to the number of elements in the data structure.
- All queue and deque methods should run in at worst linear time with respect to the number of elements in the data structure.
- All “peek” methods should run in constant time with respect to the number of elements in the data structure.
Task 1.
Implement the ArrayDeque constructors as above and methods as per the specifications in the interfaces/IDeque.java, interfaces/IQueue.java and interfaces/IStack.java files.
LinkedDeque Requirements
Your LinkedDeque class should implement the IDeque, IQueue, and IStack interfaces using linked nodes to store the data.
Your data structure should initially be empty (you must represent an empty deque with a null head) and should add/remove nodes one at a time as needed.
You should also override the toString method to output the canonical list representation we used in lecture. You should implement the following constructor:
public LinkedDeque()
Initializes an empty LinkedDeque.
When you choose the design of your LinkedDeque, keep the following restrictions in mind:
- All stack, queue, and deque methods should run in constant time with respect to the number of elements in the data structure.
- All “peek” methods should run in constant time with respect to the number of elements in the data structure.
Your Node class will need to be “doubly linked” (prev pointers in addition to next pointers) to meet these time requirements. Think about if your
LinkedDeque needs any extra fields to meet the time requirements as well. In particular, you should avoid loops in all of the add and remove methods.
Task 2.
Implement the LinkedDeque constructor as above and methods as per the specifications in the interfaces/IDeque.java, interfaces/IQueue.java and interfaces/IStack.java files.
CircularArrayFixedSizeQueue Requirements
If we further restrict ourselves to data structures with a fixed number of elements, then there is a clever way to implement a queue using an array as the backing data structure. The idea is to keep indices that point to the current “front” and “back” of the queue (which may not be the first and last indices!).

As we add to the queue, we move the back index forward (wrapping around if necessary), and as we remove from the queue, we move the front index forward (wrapping around if necessary). If there is no space to add an element, we cowardly refuse to add it and return false to signal that the operation was unsuccessful.
Your CircularArrayFixedSizeQueue class should implement the IFixedSizeQueue interface using a backing array to store the data.
Your data structure should never change capacity. You should also override the toString method to output the canonical list representation we used in lecture.
You should implement the following constructor:
public CircularArrayFixedSizeQueue(int capacity)
Initializes the CircularArrayFixedSizeQueue with a capacity of capacity.
All operations should run in constant time with respect to the number of elements in the data structure.
You are limited to 3 fields for this data structure. This means you will need to consider carefully which things to choose as fields. The fields don’t have to be exactly the “obvious” ones.
Task 3.
Implement the CircularArrayFixedSizeQueue constructor as above and methods as per the specification in the interfaces/IFixedSizeQueue.java file.
Modelling a Guitar String
When a guitar string is plucked, the string vibrates and creates sound. The length of the string determines its fundamental frequency of vibration. We model a guitar string by sampling its displacement (a real number between -1/2 and +1/2) at \(n\) equally spaced points in time. The integer \(n\) equals the sampling rate (44,100 Hz) divided by the desired fundamental frequency, rounded up to the nearest integer. The vibrations that result from plucking the string spread wave-like over time. This spreading can be simulated using the Karplus-Strong algorithm.
In one step of the Karplus-Strong algorithm, we delete the first sample from the queue, and add a new value to the end of the queue that is equal to the average of the deleted sample and the new first sample, scaled by an energy decay factor, which we will set to 0.996. Over multiple steps of this algorithm, it serves as a gentle low-pass filter (which removes higher frequencies while allowing lower frequencies to pass). Because it is in the path of the feedback, this has the effect of gradually attenuating the higher harmonics while keeping the lower ones, which corresponds closely to the sound that a guitar makes when plucked. Below we see a diagram detailing one iteration of the Karplus-Strong algorithm:
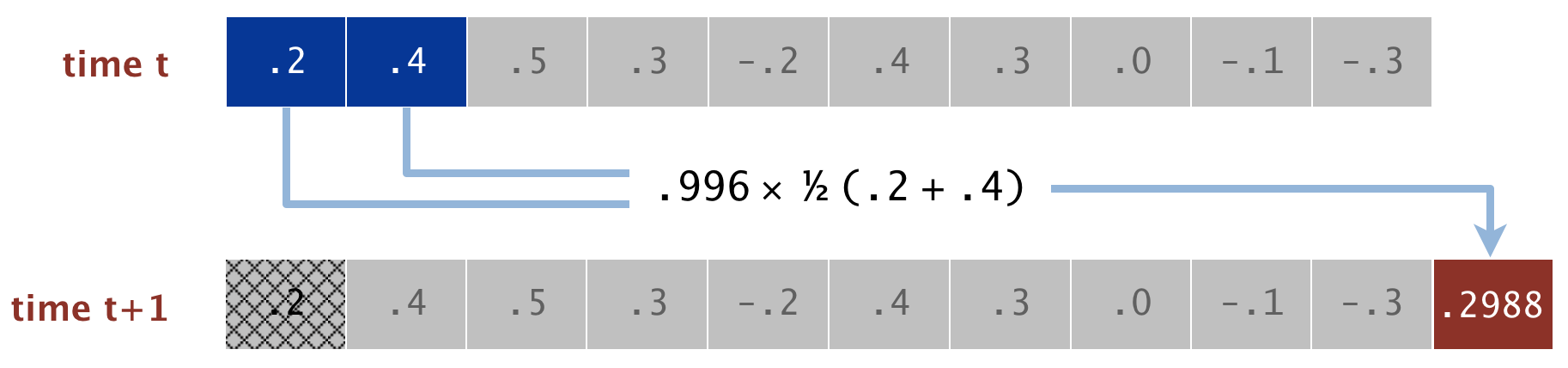
The CircularArrayFixedSizeQueueGuitarString class implements this model. You should to implement the following constructor and methods:
public CircularArrayFixedSizeQueueGuitarString(double frequency)
Creates a guitar string of the specified frequency, using a sampling rate of 44,100.
To do this, you should create a CircularArrayFixedSizeQueue of the desired capacity (the sampling rate 44,100 divided by the frequency, rounded up to the nearest integer), and
initialize it to represent a guitar string at rest by enqueuing \(n\) zeros.
public int length()
Returns the size of the queue used to represent this guitar string.
public void pluck()
Simulates the initial pluck of the string. This should initialize all values in the queue with white noise (uniformly random values between -0.5 and 0.5).
public voic tic()
Simulates one time step forward of the string vibration. This is done by applying the Karplus-Strong algorithm to the queue.
Remove the value at the front of the queue, then add a new value that is equal to the average of the removed value and the new front value scaled by the energy decay factor, 0.996.
public double sample()
Returns the current value of the energy of the string (value at the front of the queue).
Task 4.
Implement the methods in CircularArrayFixedSizeQueueGuitarString as described above.
Running The Interactive Guitar Player
Once both the CircularArrayFixedSizeQueue and CircularArrayFixedSizeQueueGuitarString classes are complete, you should be able to run GuitarHero.
The purpose of this class is to create a simulator that supports a total of 37 notes on the chromatic scale from 110 Hz to 880 Hz. If your string and queue are implemented correct,
you should be able to play music using your keyboard as follows:
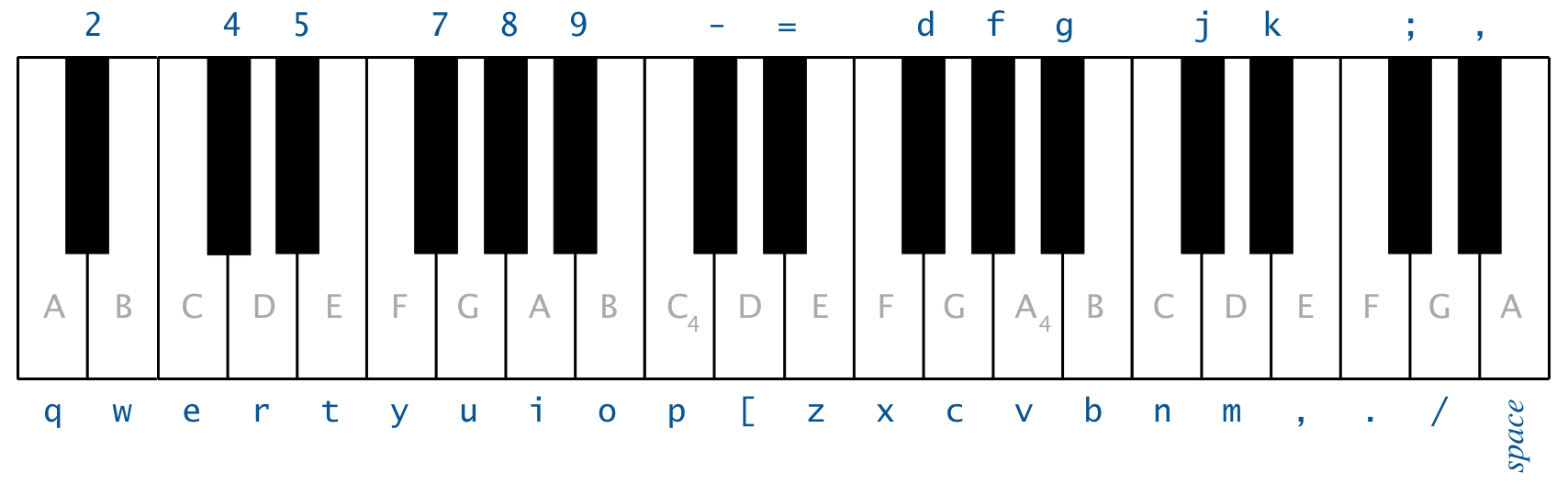
The keyboard imitates a piano, such that the white keys are on the qwerty and zxcv rows and the black keys are on the 12345 and asdf rows of the keyboard.
For each note, you should expect a sharp pluck at the beginning followed by an attenuation as the sound gets quieter.
Acknowledgements
This project is adapted from an assignment by Andrew Appel, Jeff Bernstein, Maia Ginsburg, Ken Steiglitz, Ge Wang, and Kevin Wayne.
OpenEnded Questions
Task 5. Answer all the OpenEnded questions below this task. These will be graded entirely on completion/effort, but they will really help us improve the course. Then, click the “Submit OpenEndeds” button below.
