Goals and Outcomes

In this project, you will implement the algorithms behind graph coloring and register allocation.

By the end of this project, you will…

• have implemented a heap
• have implemented an approximation to an NP-Hard problem
• understand how simple data structures can be used in combination to accomplish fairly complex tasks

Overview

You will be using the data structures you have implemented so far along with a heap to drive an algorithm for register allocation (described later).

Connection to Lecture

This project covers heaps/priority queues and basic graphs. You will likely find these lectures to be very useful in this project.

Always Forward, Never Backward

This project is the culmination of the sequence of projects we’ve done in the past few weeks. As such, it relies on these projects (mostly) working. In particular, we now absolutely expect you to have two working IDeque implementations (ArrayDeque and LinkedDeque).

Additionally, ChainingHashDictionary and MoveToFrontDictionary will be necessary in all the parts this week.

Implementing an IPriorityQueue: MinFourHeap

Your MinFourHeap should be an implementation of the heap data structure we’ve discussed in class. It should be an array-based implementation which starts at index 0. Unlike the implementation discussed in lecture, it should be a four-heap (not a two-heap). In other words, each node should have four children, not two. All operations should have the efficiencies we’ve discussed in class.

All elements of your MinFourHeap will be of type PQElement which has a data field and a priority field. The priority field is how your MinFourHeap should order elements, but the data field is how you should test equality of elements.

We are asking you to implement decreaseKey and increaseKey which operate on the key but need access to the index. This means one of your fields should be an IDictionary that maps keys to their current indices in the heap. You do not, however, have to implement an iterator for your MinFourHeap.

Graph Coloring and DSatur

What is Graph Coloring?

Graph coloring is an assignment of labels (called ‘colors’ because they lend themselves well to visualization) to graph elements and can be done according to various constraints. The most common form, and the one we’ll focus on here, is coloring the vertices of a graph such that no two vertices connected by an edge share the same color. For an example, see the graph coloring wiki.

This is a useful formulation for problems like scheduling (where jobs (“vertices”), some of which may require shared resources (“edges”), must be scheduled into time slots (“colors”) such that there are no conflicts (more than one job that needs a particular resource in the same time slot)), computer register allocation (more on this below), pattern matching, and even solving Sudoku puzzles! It’s trivial to find any valid coloring (e.g., assign each vertex its own color), so the goal becomes to color a graph using the fewest possible colors (e.g., want schedule of jobs to take up as few time slots as possible). An optimal coloring is an assignment that uses the least possible number of colors for a given graph. Further examples can be found at the bottom of this page–these are some of the graphs that we will test your code on!

Intractability of Exact Graph Coloring

Exact solutions to graph coloring are “NP-hard”, meaning we do not have any polynomial runtime algorithm that can optimally color a graph. Approximate algorithms attempt to produce near-optimal colorings in practical runtimes, and for some graphs can discover an optimal solution. A common approximate algorithm is greedy coloring, in which one iterates over the nodes (in some order) and assigns each node the lowest color available (unused by any of its neighbors) until all nodes are colored. It turns out that generally, we can do better than this by ordering the nodes using a PriorityQueue!

A Pretty Good Algorithm

DSatur is an approximate graph coloring algorithm that determines the next vertex to color via a “degree of saturation” heuristic. For a vertex v, the degree of saturation is defined as the number of unique colors across v’s neighbors. Intuitively, the vertices touching the most colors have the strongest constraints on which color they can take on, and so should be assigned a color before those with weaker constraints in order to minimize the total number of colors used. DSatur is known to find exact solutions on bipartite, cycle and wheel graphs.

• Algorithm:
  • Create a PriorityQueue with vertex labels (ints) with priorities according to their degrees of saturation
  • While there is a vertex that is not colored:
    • Dequeue the vertex with the largest degree of saturation
      • To tiebreak, take the vertex with the larger number of uncolored neighbors
      • Our tests require that you never deprioritize vertices, i.e., you should only ever call decreaseKey()
    • Color it with the lowest possible color not already in use by any neighbors
    • Update the priorities of any uncolored neighbors

DSatur: Example Walkthrough

Consider the following wheel graph. DSatur is guaranteed to optimally color wheel graphs (i.e., minimum number of total colors possible). We will walk through an example DSatur() algorithm execution. This exact graph is in the tests.

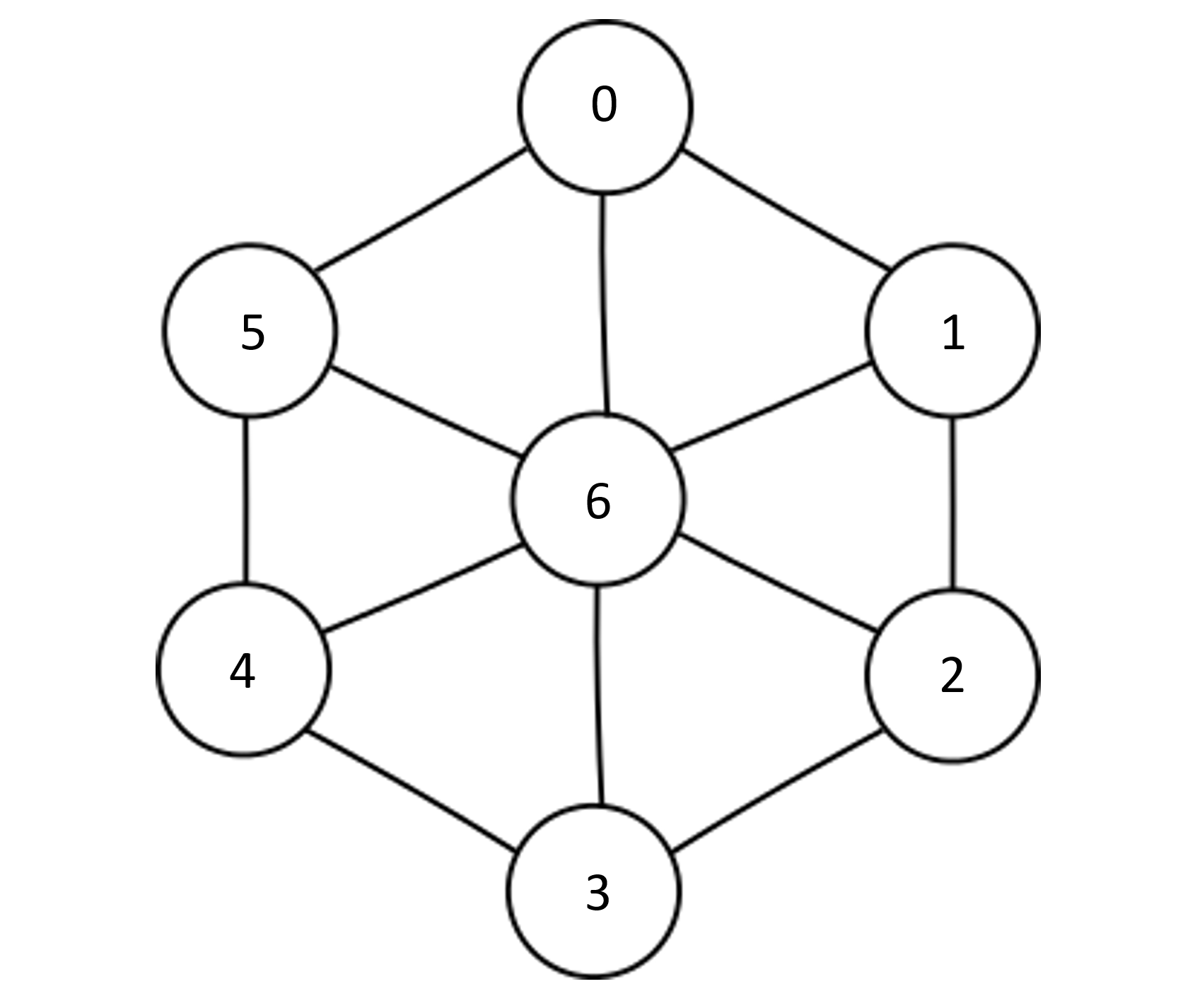
1. Make a PQ, add each vertex 0 - 6 in order with corresponding degree of saturation. All vertices have 0 colored neighbors at the start, but we add the tiebreaking term. Because the center node 6 has the largest number of uncolored neighbors, it will have the first priority. All others have equal priority.
2. Dequeue 6 from PQ. Assign it color 1 as this is the lowest available color of all of its neighbors.
3. Update the priority of each of 6’s neighbors (all have +1 colored neighbors).
4. All uncolored vertices have equal priorities now. Dequeue 5 from the top of the heap (should be on top, as it was added last in step 1, and when vertex 6 is dequeued, PQ puts the last element in 6’s place at top and then percolates it down if need be).
5. Assign 5 color 2, as this is the lowest available color given its neighbor 6 is already assigned color 1.
6. Update the priorities of 5’s neighbors, 4 and 0. These will now have the lowest priority as they have the largest number of colored neighbors (2), vs. 1 everywhere else.
7. Dequeue 4 next and assign it color 3, as it touches both 5 (color 2) and 6 (color 1). Update priority of 3. 3 and 0 will now have equal priorities.
8. Dequeue 3 next and assign it color 2, as it touches both 4 (color 3) and 6 (color 1). Update priority of 2.
9. Dequeue 2 next and assign it color 3, as it touches both 3 (color 2) and 6 (color 1). Update priority of 1.
10. Dequeue 1 next and assign it color 2, as it touches both 2 (color 3) and 6 (color 1). Update priority of 0 (stays the same).
11. Dequeue 0 last and assign it color 3 as it touches 1 (color 2), 5 (color 2), and 6 (color 1).
12. We have colored all vertices and found an optimal 3-coloring! We are done.

Interference Graphs and Register Allocation

Registers and Register Allocation

Registers are very small amounts of memory (on the scale of 32, 64 bits) which can be accessed very quickly. Because of this, programs run faster when as many variables as possible can be put into the registers. A computer processor has a limited number n registers (often in range of 8 to 32), so the results of operations have to be shuttled back and forth from RAM (or elsewhere) to maximally utilize the registers. If you’d like to learn more about this, take CS 24!

Because registers are a limited resource but can significantly speed up computation, determining how to optimally allocate them is an important question! This is the goal of register allocation: deciding which variables to store in which registers, and when. It turns out that this can be (and is) framed as a graph coloring problem!

A Simplification of Programs

Although programs are written in coding languages which contain a large set of possible instructions (e.g., Java), the compiler translates these languages to a smaller set of base instructions that the computer can execute. These base instructions are very simple and can be performed in the registers. Examples include writing a variable, reading a variable, and various mathematical operations.

As we’d like to do register allocation, we will only pay attention to read and write instructions because these define when a variable is “live” (i.e., in use) and needs to be stored in a register. A variable is considered live if there has been an instruction to read it (onto a register) or if it’s being referenced by the current instruction (need to bring it onto a register if not already present). A variable stops being live when it gets written out of the register (back into RAM or other slower memory). Note that, somewhat unintuitively, a read puts a variable onto a register, whereas a write removes a variable from a register.

Variable Interference in Programs

Finally: we want to assign each variable in a program to a specific register. Generally, each register can only store one variable at a time. Thus, variables that are live at the same time in the program cannot be stored in the same register. To represent this, we can construct a variable interference graph: if two variables are live at the same time, they “interfere” and must be placed on different registers (i.e., they need to be colored differently). If two variables don’t interfere at all in the course of program execution, we can make more efficient use of our registers by putting the second variable on the same register as the first, once the first is no longer live. Once we construct this interference graph, we can simply run our graph coloring algorithm on it to match registers to variables!

Constructing the Interference Graph

• Algorithm:
  • Create a new list of instructions where the program is “backwards”. The idea here is that we want to determine when a variable was last used; so, we need to go through the program backwards.
  • We consider a variable to be “written” if there has been a write instruction, but no corresponding read instruction yet.
  • For each instruction:
    • If it’s a read instruction, the variable is no longer “written”!
    • If it’s a write instruction, the variable is now “written”!
    • A variable is considered live if it’s “written” OR referenced in the current instruction.
    • For all non-equal pairs of live variables:
      • Add an edge to the interference graph (indicating they are “in use” at the same time).
  • Return the interference graph

Interference Graph Construction: Example Walkthrough

Consider the following program: p = [Read 0, Read 1, Write 0, Read 2, Read 3, Write 1, Write 2, Write 3]. This is the first program you are tested on.

1. Initialize new NodeGraph of size 4 (as there are 4 unique variables, {0, 1, 2, 3}).
2. Construct reverse_p = [Write 3, Write 2, Write 1, Read 3, Read 2, Write 0, Read 1, Read 0].
3. Initialize an empty set live.
4. Go through each instruction in reverse_p:
   • Write 3: add 3 to live. There are no other live variables yet so do nothing.
   • Write 2: add 2 to live. 3 is also live, so add an edge between (2,3).
   • Write 1: add 1 to live. 2,3 are also live, so add an edge between (1,2) and (1,3).
   • Read 3: remove 3 from live. No new edges to create.
   • Read 2: remove 2 from live. No new edges to create.
   • Write 0: add 0 to live. 1 is also still live, so add an edge between (0,1).
   • Read 1: remove 1 from live. No new edges to create.
   • Read 0: remove 0 from live. No new edges to create.
5. Return your graph!
6. Draw the graph out for yourself to see that this can be optimally colored using only 3 colors (i.e., registers).