Goals and Outcomes

In this project, you will build a guitar simulator which synthesizes guitar-like sounds using various data structures.

By the end of this project, you will…

• gain an understanding of the usage of backing arrays and linked lists in data structures
• learn multiple methods of implementing a stack, queue, and deque and analyze the pros/cons of each method
• understand the power of abstraction in breaking down a problem and implementing a solution

Connection to Lecture

This project is covers lecture03 through lecture06. You will likely find the code from these lectures to be very useful in this project.

Overview and Implementation Strategy

In the previous two projects, you were a client of the built-in Java data structures in java.util. One of the main goals of the next series of projects is to build your own versions of these data structures (i.e., be the implementor rather than the client). In this project, you will begin this process by building your own versions of the list-like structures. In particular, you will implement three different versions of stacks and queues.

After you’ve implemented the data structures, you will build a program to simulate the plucking of a guitar string. Your sound synthesizer will use your data structures to back the algorithm.

Stacks, Queues, and Deques

We saw stacks and queues in lecture, but, in this project, you will implement a generalization of them called a deque (prounounced “deck”). A deque is a “double-ended queue” which allows you to add and remove from both ends. Another way of looking at deques is that they are simultaneously stacks (LIFO data structures) and queues (FIFO data structures). Just like with lists, there are multiple implementations of deques: an array-based implementation and a node-based implementation. We will begin with implementing these.

ArrayDeque Requirements

Your ArrayDeque class should implement the IDeque, IQueue, and IStack interfaces using a backing array (not an ArrayList!) to store the data. Your data structure should have a default initial capacity of 10 items and grow when it runs out of internal capacity. You should also override the toString method to output the canonical list representation we used in lecture. You should implement the following two constructors:

public ArrayDeque()

Initializes the ArrayDeque with the default initial capacity of 10.

public ArrayDeque(int initialCapacity)

Initializes the ArrayDeque with the initial capacity of initialCapacity.

One of your constructors should call the other one using the this() notation discussed in lecture. The tests will check for this.

public OurArrayList(int initialCapacity) {
    this.data = (E[])new Object[initialCapacity];
    this.size = 0;
}

public OurArrayList() {
    this(10);
}

When you choose the design of your ArrayDeque, keep the following restrictions in mind:

• All stack methods should run in constant time with respect to the number of elements in the data structure.
• All queue and deque methods should run in at worst linear time with respect to the number of elements in the data structure.
• All “peek” methods should run in constant time with respect to the number of elements in the data structure.

LinkedDeque Requirements

Your LinkedDeque class should implement the IDeque, IQueue, and IStack interfaces using linked nodes to store the data. Your data structure should initially be empty (you must represent an empty deque with a null head) and should add/remove nodes one at a time as needed. You should also override the toString method to output the canonical list representation we used in lecture. You should implement the following constructor:

public LinkedDeque()

Initializes an empty LinkedDeque.

When you choose the design of your LinkedDeque, keep the following restrictions in mind:

• All stack, queue, and deque methods should run in constant time with respect to the number of elements in the data structure.
• All “peek” methods should run in constant time with respect to the number of elements in the data structure.

CircularArrayFixedSizeQueue Requirements

If we further restrict ourselves to data structures with a fixed number of elements, then there is a clever way to implement a queue using an array as the backing data structure. The idea is to keep indices that point to the current “front” and “back” of the queue (which may not be the first and last indices!).

As we add to the queue, we move the back index forward (wrapping around if necessary), and as we remove from the queue, we move the front index forward (wrapping around if necessary). If there is no space to add an element, we cowardly refuse to add it and return false to signal that the operation was unsuccessful.

Your CircularArrayFixedSizeQueue class should implement the IFixedSizeQueue interface using a backing array to store the data. Your data structure should never change capacity. You should also override the toString method to output the canonical list representation we used in lecture. You should implement the following constructor:

public CircularArrayFixedSizeQueue(int capacity)

Initializes the CircularArrayFixedSizeQueue with a capacity of capacity.

All operations should run in constant time with respect to the number of elements in the data structure.

Modelling a Guitar String

When a guitar string is plucked, the string vibrates and creates sound. The length of the string determines its fundamental frequency of vibration. We model a guitar string by sampling its displacement (a real number between -1/2 and +1/2) at \(n\) equally spaced points in time. The integer \(n\) equals the sampling rate (44,100 Hz) divided by the desired fundamental frequency, rounded up to the nearest integer. The vibrations that result from plucking the string spread wave-like over time. This spreading can be simulated using the Karplus-Strong algorithm.

In one step of the Karplus-Strong algorithm, we delete the first sample from the queue, and add a new value to the end of the queue that is equal to the average of the deleted sample and the new first sample, scaled by an energy decay factor, which we will set to 0.996. Over multiple steps of this algorithm, it serves as a gentle low-pass filter (which removes higher frequencies while allowing lower frequencies to pass). Because it is in the path of the feedback, this has the effect of gradually attenuating the higher harmonics while keeping the lower ones, which corresponds closely to the sound that a guitar makes when plucked. Below we see a diagram detailing one iteration of the Karplus-Strong algorithm:

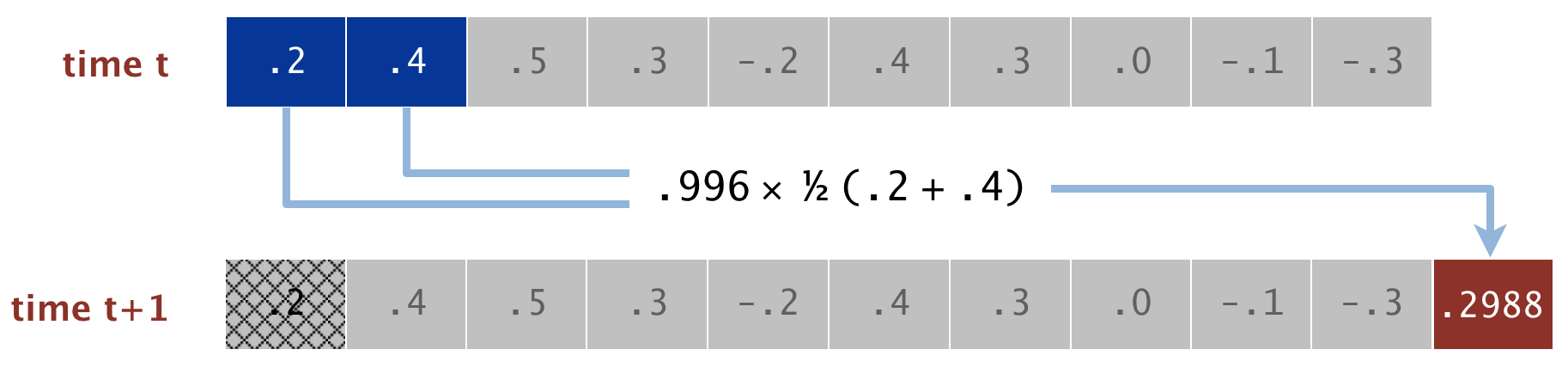
The CircularArrayFixedSizeQueueGuitarString class implements this model. You should to implement the following constructor and methods:

public CircularArrayFixedSizeQueueGuitarString(double frequency)

public int length()

Returns the size of the queue used to represent this guitar string.

public void pluck()

Simulates the initial pluck of the string. This should initialize all values in the queue with white noise (uniformly random values between -0.5 and 0.5).

public void tic()

public double sample()

Returns the current value of the energy of the string (value at the front of the queue).

Running The Interactive Guitar Player

Once both the CircularArrayFixedSizeQueue and CircularArrayFixedSizeQueueGuitarString classes are complete, you should be able to run GuitarHero. The purpose of this class is to create a simulator that supports a total of 37 notes on the chromatic scale from 110 Hz to 880 Hz. If your string and queue are implemented correct, you should be able to play music using your keyboard as follows:

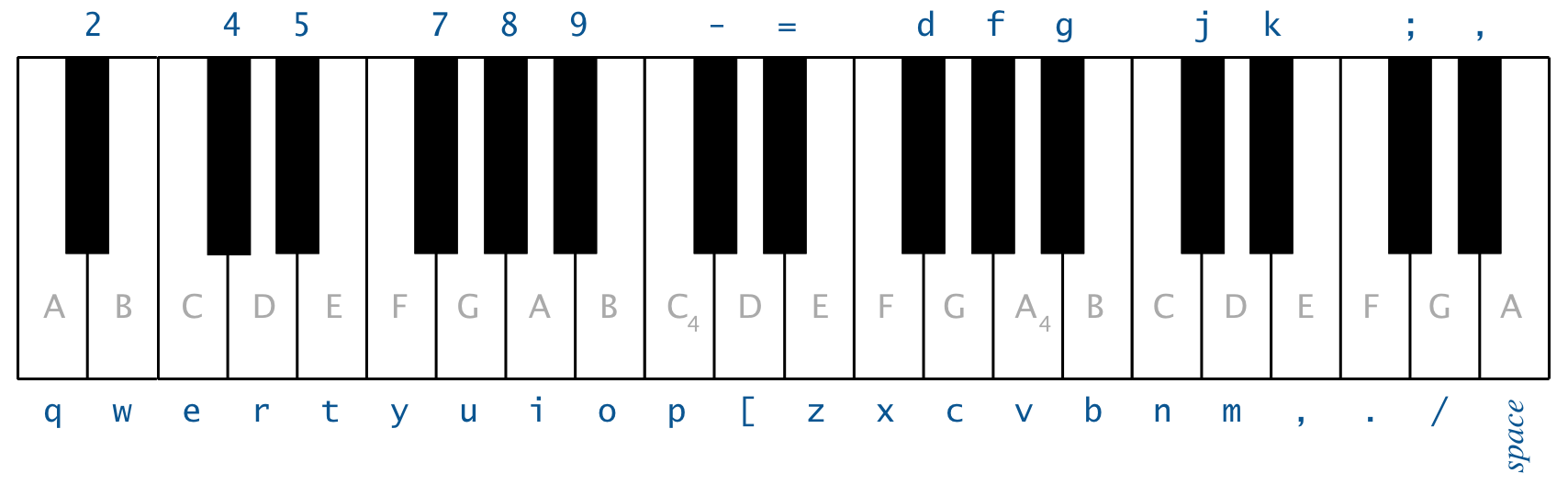
The keyboard imitates a piano, such that the white keys are on the qwerty and zxcv rows and the black keys are on the 12345 and asdf rows of the keyboard. For each note, you should expect a sharp pluck at the beginning followed by an attenuation as the sound gets quieter.

Acknowledgements

This project is adapted from an assignment by Andrew Appel, Jeff Bernstein, Maia Ginsburg, Ken Steiglitz, Ge Wang, and Kevin Wayne.